|
|
|
Klein'sche Flasche, Möbius Band |
Chaostheorie und Attraktoren |
Fraktale Dimension, Cantor Menge |
Mandelbrot Menge, Feigenbaum-Diagramm |
Schneeflocken Kurve, Sierpinski-Dreieck |
Bifurkation und Feigenbaum-Szenario |
Hilberts Hotel, Hilbert Kurve |
Penrose-Parkettierung |
Künstlerische Dartsellung: Maurits Cornelis Escher
|
| |
|
|
 |
|
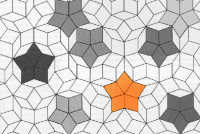
Penrose Parkettierung (Fliesen)
Der britische Physiker Sir Robert Penrose entdeckte 1974, dass man durch
Kombination von nur zwei geometrischen Figuren (sogenannter "Kites" und "Darts")
bei Einhaltung bestimmter Legeregeln eine unendlich grosse Fläche
bedecken kann, ohne dass sich einzelne Teilausschnitte je wiederhohlen.
Jede so mögliche Parkettierung ist nichtperiodisch, d.h. sie kann durch
keine Verschiebung zur Deckung mit sich selbst gebracht werden.
Roger Penrose ist Rouse-Ball-Professor für Mathematik an der
Universität Oxford und Mitglied der Royal Society.
Zu seinen zahlreichen Auszeichnungen zählt der Wolf-Preis der
Physik, den er im Jahre 1988 zusammen mit Stephen Hawking für
gemeinsame Beiträge zur Kosmologie, insbesondere für die
Theorie der Schwarzen Löcher
erhalten hat. Ausserdem hat er die nach ihm benannte nichtperiodische
Parkettierung der Ebene entdeckt.
Bei der Penrose-Parkettierung handelt es sich um eine sog.
Quasikristall-Struktur. Ein Kristall ist ein hochsymmetrisches Gitter
aus Atomen und Molekühlen in einem ständig wiederkehrenden Muster.
Bei einem Quasikristall entspricht das kristalline Muster keiner bekannten
möglichen drei-dimensionalen Kristallstruktur. Hier fehlt die präzise
Regelmäßigkeit eines echten Kristalls.
Erst im höherdimensionalen Raum wird die Symmetrie der Quasikristalle sichtbar.
Die Penrose-Parkettierung zeigt die Projektion einer fünf-dimensionalen
Kristallstruktur auf nur zwei Dimensionen.
|
|
|
| © Dagmar Kuntz, 1998-2026 |
